Two Dimensional Coordinate Systems are a method of describing a point in a plane using an ordered pair of numbers $(n_1,n_2)$ called coordinates such that $n_1$ = constant is a set of non-intersecting lines (or curves). Similarly, $n_2$ = constant produce a second set of non-intersecting lines (or curves). Therefore the ordered pair of numbers indicate a point located at the intersection of a pair of the lines (or curves), one from each set.

A special class of coordinate systems are those where each line of one set intersect at right angles to every line of the other set. Such a system is called an Orthogonal Coordinate System.

Here are some orthogonal coordinate systems in two dimensions

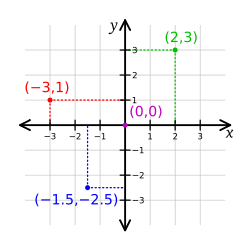Cartesian Coordinate System
- Coordinate curves are both straight lines
- named after the inventor of the system René Descartes
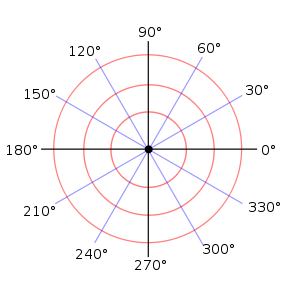Polar Coordinate System
- Coordinate curves are circles and straight lines
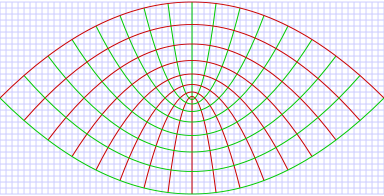Parabolic Coordinate System
- Coordinate curves are both parabolas
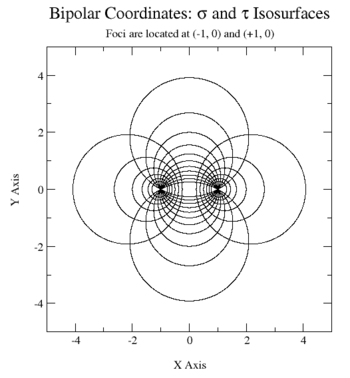Bipolar Coordinate System
- Coordinate curves are both circles
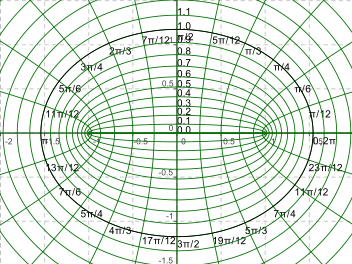Elliptic Coordinate System
- Coordinate curves are ellipses and hyperbolae

By extension Coordinate Systems exist for three and more dimensions.

Last change to this page
Full Page history
Links to this page
 Edit this page
  (with sufficient authority)
Change password
 Recent changes
All pages
Search