AxiomYou are currentlybrowsing as guest. Click here to log in |
|
||||||||
AxiomYou are currentlybrowsing as guest. Click here to log in |
|
||||||||
An axiom (or postulate) is any mathematical statement that is the starting point from which other statements (often called theorems) are logically derived.
Axioms are considered self-evident requiring neither proof nor justification.
Many areas of mathematics are based on axioms: set theory, geometry, number theory, probability, etc.
At the start of 20th Century Mathematicians showed great confidence in the development of the axiomatic foundations of Mathematics. However this confidence was shattered by the work of Kurt Goedel.
One requirement of an axiomatic system is that it is consistent i.e. does not lead to contradictory theorems - thus creating a paradox (see Russell's Paradox).
|
In Euclidian Geometry the 5th (or parallel) postulate states:
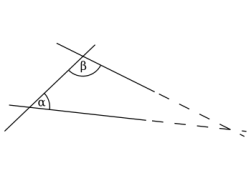
However Nikolai Lobachevsky (1792 - 1856) and JŠnos Bolyai (1802 - 1860) considered this axiom was not self-evident. When they investigated the effect of substituting an alternative axiom such that lines do not meet, however far extended, found no resulting contradictions thus formulating the first non-Euclidian Geometry. This Geometry (called hyperbolic geometry) has many features different from Euclidean Geometry. For example, the sum of the angles of a triangle is less than 180 degrees and the greater the area of the triangle the smaller the sum. Poincare's Disc is a model of such a geometry.
Different axioms lead to different geometries. Mathematics thus supplies a number of competing descriptions of Space, the correct interpretation being found experimentally. The descriptions of Space by Albert Einstein and others requires Space to be non-Euclidean.
|
Last change to this page Full Page history Links to this page |
Edit this page (with sufficient authority) Change password |
Recent changes All pages Search |